Clusterização de dados
Introdução
Clusterização ou aprendizado não supervisionado, é uma das técnicas mais importantes em análise de dados [1]. Técnicas de clusterização buscam encontrar padrões naturais inerentes aos dados, agrupando dados não rotulados em grupos homogêneos, chamados de Clusters. Dados de um mesmo cluster são mais similares entre si e menos similares em relação a dados de outros clusters.
As técnicas de clusterização tem sido amplamente aplicadas nas áreas de mineração de dados, segmentação de imagens, reconhecimento de padrões, pesquisa de mercado, etc. [2].
Abordagens tradicionais de clusterização são divididas em dois grupos principais: algoritmos hierárquicos e algoritmos de partição. Algoritmos hierárquicos são capazes de encontrar clusters aninhados de modo aglomerativo, de maneira que os pontos de dados mais similares são fundidos recursivamente até formar uma hierarquia de clusters, e divisivo onde todos os dados começam em um mesmo cluster e então são divididos recursivamente em clusters menores. Algoritmos de partição encontram simultaneamente todas as partições de dados sem impor qualquer estrutura hierárquica [1]. Dentre os métodos mais comuns de algoritmos de partição temos: K-Means, Mean-Shift, DBScan e Expectation-Maximization usando modelos de misturas gaussianas.
Dentre todas as abordagens de clusterização, a mais difundida e utilizada, mas, não necessariamente a melhor, é o K-Means. O K-Means é um algoritmo simples e que em termos gerais funciona razoavelmente bem para muitas aplicações. Neste artigo pretendo explicar o conceito de funcionamento do K-Means, seu comportamento em algumas bases de dados e como poderíamos estimar automaticamente o número de cluster uma vez que este método exige como entrada um número definido de cluster.
K-Means
O método K-Means foi proposto por MacQueen em 1967. Consiste em inicializar um conjunto de K centroides (ou protótipos) que caracterizam o conjunto de dados. Os dados são atribuídos ao centróide mais próximo baseado em alguma medida de distância (Euclidiana é a mais comum). O objetivo do método é minimizar a função da soma dos erros quadráticos (Eq.1) através da atualização dos centróides (Eq.2) de forma iterativa até que seja alcançado um critério de convergência.
\(J = \sum^k_{i=1}{\sum_{x \in C_i}{||x - \mu(C_i)||^2}}\) (1)
onde \(k\) é número total de clusters, \(\mu(C_i)\) é o centroide do cluster \(C_i\) e \(\vert \vert x - \mu(C_i)\vert \vert^2\) calcula a distância entre a amostra \(x\) e o centróide \(\mu(C_i)\) ao qual ela pertence (está mais próxima).
\(\mu(C_i) = \frac{1}{n_i} \sum_{x \in C_i}{x}\) (2)
\(n_i\) é o número total de amostras \(x\) pertencentes ao centróide \(C_i\).
O pseudo-código pode ser visualizado logo abaixo:
Pseudo-código: K-Means
(1) Inicializar K centróides representando o grupo de clusters inicial.
(2) Atribui cada objeto ao centróide mais próximo.
(3) Recalcular a posição dos centróides de acordo com a eq. (2).
(4) Repetir os passos (2) e (3) até alcançar um critério de convergência.
Clusterizando uma base de dados
Para ilustrar o comportamento do K-Means no processo de agrupamento dos dados, foi selecionada a imagem abaixo como nossa base de dados a ser clusterizada.

Uma imagem RGB consiste em uma matriz tri-dimensional com 3 camadas de cores. No entanto, para a clusterização com o K-Means a relação espacial dos pixels pouco importa, logo a imagem RGB pode ser convertida para uma matriz com 3 colunas, sendo cada coluna pertencente a uma cor. A imagem abaixo exemplica esse processo.
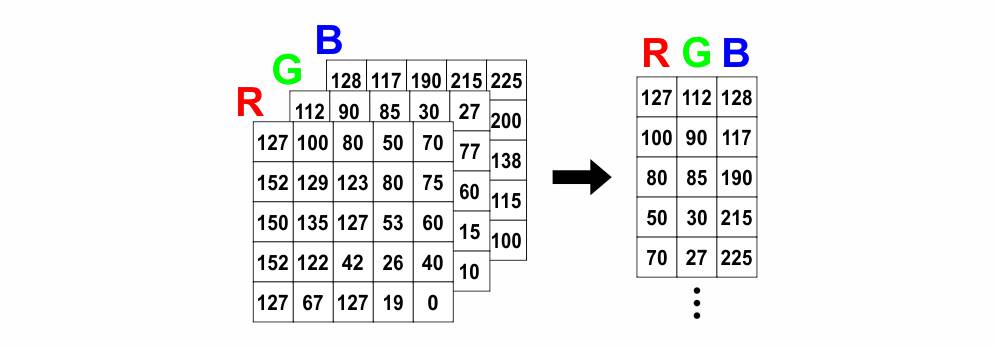
Abaixo segue um código simplificado e comentado sobre a utilização do K-Means na clusterização de imagens.
# Importa os módulos necessários
import numpy as np
from skimage import io
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
# Lê a imagem de entrada
img = io.imread('folha-de-cafe.jpg')
# Salva dimensões da imagem
dim = img.shape
# Converte para um vetor bidimensional que será processado pelo kmeans
data = img.reshape(-1, 3)
# Inicializa o K-Means com 4 clusters e com centróides aleatórios
kmeans = KMeans(n_clusters=4, init='random')
# Chama o método .fit() para agrupar os dados
kmeans.fit(data)
# Retorna os rótulos para cada pixel/instância
labels = kmeans.labels_
# Retorna o valor de cada centroid
centroids = kmeans.cluster_centers_
# Converte para inteiros entre 0 e 255
centroids = np.uint8(centroids)
# Substitui os valores dos dados com o valor do centroid a que pertencem
for i in np.unique(labels):
data[np.where(labels == i), :] = centroids[i, :]
# Retorna os dados para a dimensão original
img = data.reshape(dim)
# Imprime a imagem resultante
plt.imshow(img)
Como resultado nós obtemos a seguinte imagem após a clusterização com o K-Means:
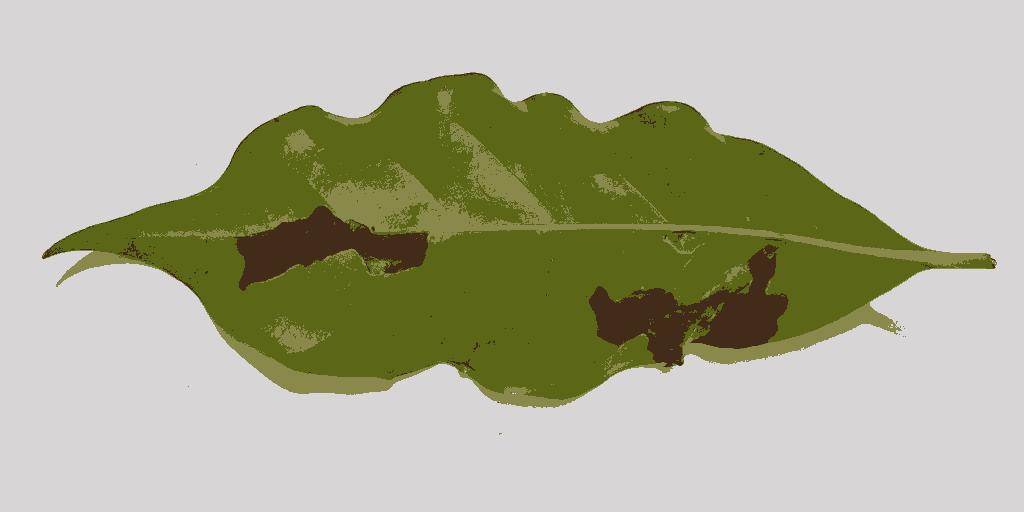
[1] JAIN, Anil K. Data clustering: 50 years beyond K-means. Pattern recognition letters, v. 31, n. 8, p. 651-666, 2010.
[2] JAIN, Anil K.; MURTY, M. Narasimha; FLYNN, Patrick J. Data clustering: a review. ACM computing surveys (CSUR), v. 31, n. 3, p. 264-323, 1999.